たにしきんぐダム

プログラミングやったりゲームしてます

Coursera の Algorithms on Strings 受けました

アルゴリズム tech

Cousera の Algorithms on Strings を受講していて、平日にお昼ご飯食べながらビデオを見たり休日とかに課題をやったりしていたのですが先日完走しました！(講義は4週分なのですが忙しかったり難しかったりで2ヶ月くらいかかってしまった)
お金を払うと課題提出システムみたいなのが使えて提出したプログラムの時間/空間計算量を教えてくれるらしいけど無料でも授業ビデオと資料にはアクセスできた
めちゃくちゃ良かったのでみんなも受講しましょう

www.coursera.org

きっかけはアルバイト先で開催されていたのに参加させてもらったのと、 ISUCON6予選で高速な文字列マッチングアルゴリズムが全く分からず悔しい思いをしたから(正規表現の更新・キャッシュをうまく頑張れば十分な点数は獲得できたみたいですが...)でした。
学んで終わりじゃ多分忘れるから何とか応用とかできたら良い

授業ビデオは例を交えて教えてくれたり定理を証明してくれたりクイズが挟まったり(前半の)先生のテンションが異常に高かったりして楽しかったし分かりやすかったので受講しましょう

文句を言うならWeek4は先生がひたすらスライド数枚で定理と証明を延々と喋ったあとアルゴリズムはこれだよってスライドが何枚か出てきただけだったのはめちゃくちゃ分かりにくかったのでもっと例が欲しかった。Couseraのフォームから意見を送ったりした、評価-1したりした...
(授業ビデオに対して気軽にLike/Dislikeしたり意見を送信できるシステムがあるのは凄く良いですね)

以下は授業メモを清書したもの、ブログ書くつもりで授業受けると他の人も読むのでしっかり整理する必要があって理解が深まるという知見が！
この記事頑張りすぎたので次からはもう少し手を抜きたい

  • ちまちま書いてたらめちゃくちゃ長くなってしまったので読むとしたら辞書的に使うのが良さそう
  • この記事にはプログラムは掲載していません
  • この記事では詳細なアルゴリズムなどは書いていません(調べれば/受講すれば出てくる)、アルゴリズム・データ構造の具体例くらいの気持ち
  • この記事を読んで各アルゴリズムの雰囲気を掴んでもらって、詳しく知りたい場合はCoursera受けてみてください

Week1

BruteForce

  • ある文字列に対して複数のパターンを探索するとき、一番ナイーブなのはパターンを1つずつマッチさせていく方法で当然遅い
  • 時間計算量 = O(|Text| * |Patterns|)

Trie

  • Trieは文字列集合を表すのに適したデータ構造
  • Trieを構築すると、文字列への1度の走査で複数パターンを同時に検索することができるようになる
  • メモリ使用量が大変

これは and, anana, anntena から作ったTrie

f:id:tanishiking24:20161218022239p:plain

  • 検索対象の文字列の開始位置をずらしながら、構築したTrieを辿らせて葉節点にたどり着いたらマッチ
  • 例えば nands という文字列を検索すると
    • nands は最初の n の時点で辿れない
    • ands は葉節点まで辿れるのでマッチ
    • nds はマッチしない
    • ds もマッチしない
    • s も(ry
  • よってnands は2文字目を開始位置としてandを含んでいることがわかる
  • 時間計算量 = O(|Text| * |LongestPattern|)

Suffix Trie

  • パターンではなく探索対象の文字列のSuffixesからTrieを構築、文字列の最後に終端文字をつける($と書く)
  • 例えば nana という文字列からは
    • nana$
    • ana$
    • na$
    • a$
  • からTrieを構築
  • 葉節点には文字列の開始位置を入れておく
  • 空間計算量: |Text| * (|Text|-1)/2 なので O(|Text|^2)

f:id:tanishiking24:20161218022331p:plain

  • Trieはパターンからデータ構造を作ったが、SuffixTrieでは検索対象文字列からデータ構造を作る
  • 文字列からパターンを検索する場合は構築したSuffixTrieを辿らせる
    • root以外のノードが受理状態なDFA、受理されなかったらマッチしない
  • 受理された時点で、そこから辿れる葉節点の数字たちがパターンが文字列内に出現する位置
  • 例えば nana から na を探索
    • 葉節点にはたどりつかず途中で止まる
    • そこから辿れる葉節点には0と2、なのでnaはnanaの0番目と2番目に出現する

Suffix Tree

  • Suffix Trie から冗長なエッジを刈り取って空間計算量を節約した木
  • nana の Suffix Tree は以下
  • 下の画像だとエッジには部分文字列が入っててメモリがもったいない(さらに節約できる)
    • 元の文字列があるのでエッジには、その部分文字列開始位置と長さを持ってればOK
  • ちなみにこういうエッジに文字列が入ってるトライをパトリシアトライという

f:id:tanishiking24:20161218022344p:plain

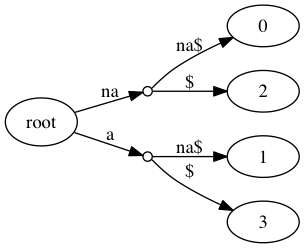
  • Suffix Tree のナイーブな構築には O(|Text|^2) かかる
  • もっと良い構築方法があり、Week4でやる
  • 葉節点の数は|Text|個、節点の数は|Text|-1個以下になるので空間計算量は O(|Text|)
    • Suffix Trie の空間計算量は O(|Text|^2) だったね

UkkonenのアルゴリズムはSuffixTreeを直接構築する(この講義ではやらない)

Week2

  • 最初に Burrows Wheeler Transform (BWT) による文字列の変換と、その逆変換のお話
  • 最後にちょっとだけ SuffixArray の話

BWT

  • 元の文字列の末尾に$(番兵)を追加
  • 一文字ずつずらして並べて
panana$
anana$p
nana$pa
ana$pan
na$pana
a$panan
$panana
  • これを辞書順にソート
$panana
a$panan
ana$pan
anana$p
na$pana
nana$pa
panana$
  • 末尾の列を見ると annpaa$ ランレングス符号化が効きそうな文字列になってる(元の文字列のBWTと呼ぶ)

BWT逆変換

  • BWTから元の文字列を復元する、辞書順にソートしたもののFirstColumnとLastColumnに注目
  • Lastの文字は常にFirstの文字の1つ手前の文字
  • Lastの$から、対応するFirstの文字、それと同一のLastの文字...って辿っていくと元の文字列が復元できる
  • 空間計算量は O(|Text|)、時間計算量も O(|Text|)
  • 各文字を一意に識別できるようにナンバリング(a0, a1 ... といった風に)
行 First Last
1 $ a0
2 a0 n0
3 a1 n1
4 a2 p0
5 n0 a1
6 n1 a2
7 p0 $
  • Lの$からスタート、対応するFはp0
  • Lのp0は4行目、対応するFは a2
  • Lのa2は6行目、対応するFはn1
  • ...
  • Lのa0は7行目、対応するFは$

BWMatching

Lastの文字は常にFirstの文字の1つ手前の文字 という性質が活きてくる

  • パターンの最後の文字から見ていく、その文字と一致するFをすべて探す
    • 一致したFに対応するLを見る、Lと同じ文字を持つFを探索範囲とする
  • パターンの後ろから2文字目を見る、その文字と一致する、探索範囲内のFを探す
    • 一致したFに対応するLと同じ文字を持つFを次の探索範囲
  • ...
  • これを繰り返してパターンの最初の文字まで見つけられたらマッチ
  • panana から pan を探索する例、後ろから n -> a -> p で調べていく
  • n に一致するFは5行目から6行目、対応するLは a1とa2
    • 次の探索範囲はFに a1 と a2 のある3行目から4行目
  • a に一致する探索範囲内のFは1行目から2行目、対応するLは n1 と p0
    • 次の探索範囲はFに n1 と p0 のある6行目から7行目
  • p に一致する探索範囲ないのFは7行目のみ、対応するLは$
    • 次の探索範囲はFに $ のある1行目
  • パターンは残ってない、この時点での探索範囲の長さ(今は1)がマッチしたパターンの数
行 First Last
1 $ a0
2 a0 n0
3 a1 n1
4 a2 p0
5 n0 a1
6 n1 a2
7 p0 $

あいまい検索をしたい場合は、探索範囲内でLastColumnがマッチしない場合でも、不一致数をインクリメントしつつも次の探索範囲に含めてあげる。不一致数が許容する不一致数に達したら次の探索範囲から外す

Suffix Array

  • 文字列の開始位置をずらした各部分文字列の開始位置
  • それを辞書順にソートしたもの

以下は panana$ の Suffix Array

sub string suffix array
$ 6
a$ 5
ana$ 3
anana$ 1
na$ 4
nana$ 2
panana$ 0
  • ナイーブにソートする場合SuffixArrayの構築には時間計算量 O(|Text|^2 * log(|Text|))
    • 長さ|Text|程度の2つの文字列の比較に|Text|と、|Text|個の文字列のソートに|Text|*log(|Text|)
  • SuffixTreeを深さ優先することでSuffixArrayを構築できる O(|Text|)
  • SuffixTreeに依存せずにもっと高速にSuffixArrayを構築することもできる(Week4)
  • SuffixArrayを使うと文字列の探索を高速に2分探索でできるようになる O(|Pattern| * log|Text|)

Week3

  • Week3で学ぶKMPでは
  • いくつかの部分文字列との比較をスキップするという理論は重要で、実用上はBoyer-Mooreのアルゴリズムとかその亜種がよく利用されるらしい。そのあたりは授業の範囲外
    • Boyer-Moore は検索対象文字列ではなくパターンに対して前処理を施すため、前処理のコストが低く、シュッとそこそこ高速に検索できる
    • しかし検索対象をインデキシングしないので同じ文書を何度も検索する場合は不向き(?)
    • GNU grep にも使われてるらしい

ShiftingPatterns

  • BruteForceアルゴリズムは、テキストがパターンと一致しなかったらテキストの開始位置をずらしてパターンと比較...を繰り返していく方法でした、時間計算量は O(|Text|*|Pattern|)
  • 実はいくつか部分文字列に対する比較をスキップできる
  • 用語定義: Border
    • 文字列のprefixとsuffixとで等しくて、その文字列本体ではないもの
    • 例
      • a は abra のborder
      • abab は ababab のborder
      • ab は ab のborder ではない (文字列本体だから)
  • abracadabra から abra という文字列を探索する例を考えてみるLongestCommonPrefix(LCP)は下の図の赤文字部分
  • ブルートフォースなら次はパターンをひとつずらして、 abracadabra に対して比較するのだが、いくつかの部分文字列に対する比較をスキップできる
  • LCPの Longest Border は下の図の青文字部分 a
    • パターンをいっきに 2つめの Longest Border (4文字目のa) の開始位置にまでずらすことができる
a b r a c a d a b r a
a b r a
a b r a

本当にこんなにスキップしちゃって大丈夫なの？？スキップした部分にパターンと一致する部分文字列あったりするんじゃないの？？
スキップした部分にパターンと一致する部分文字列が存在すると仮定すると、前提に反する結果が得られて、安全にスキップできるということが証明できる。(この記事では省略)(講義ではしっかり証明してくれます)

PrefixFunction

文字列Sに対して、Prefix Function pf(i) を、S[:i+1] の部分文字列の longest border
abababcaab の Prefix Function は以下のようになる

i 0 1 2 3 4 5 6 7 8 9
文字列 a b a b a b c a a b
pf(i) 0 0 1 2 3 4 0 1 1 2

例えば i=4のとき、部分文字列は ababa で longest border は aba なので pf(4)=3

  • ナイーブにPrefixFunctionを構築すると時間計算量O(|Text|^2)かかると思うのですが、線形時間で構築するアルゴリズムがあります。
  • PrefixFunctionはたかだか1ずつしか増加しないことに注意
  1. border=0からスタート
  2. pf(i) を求める場合は、border=pf(i-1) として
  3. Text[border] と Text[i] を比較
  4. 一致した場合はborder+=1してpf(i)=borderとしてi+1へ
  5. 不一致の場合borderを縮めて再チャレンジ(border=0の場合はpf(i)=0としてi+1へ)
    1. border=pf(border-1)として (3) に戻る

Knuth–Morris–Pratt algorithm

  • Pattern と Text を番兵で挟んで、そのSuffixArrayを作る.
  • i > |Pattern| かつ |Pattern| = pf(i) なとき、i-2*|Pattern|が元の文字列内でのマッチ部分の開始位置
i 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Pattern + $ + Text a b r a $ a b r a c a d a b r a
pf(i) 0 0 0 1 0 1 2 3 4 0 1 0 1 2 3 4
  • abracadabra から abra を探す例の場合、|Pattern|=4
  • 条件を満たすのは i=8 と i=15
    • 8-2*4=0 と 15-2*4=7が abracadabra 内での abraの開始位置、確かに
  • 時間計算量は O(|Pattern| + |Text|)
    • (PrefixFunctionの構築も、探索も O(|Pattern| + |Text|))

Week4

  • Week1ではSuffxiTreeをナイーブに構築した(時間計算量 O(|Text|^2))
  • Week2ではSuffixArrayをナイーブに構築した(時間計算量O(|Text|^2 * log(|Text|)))
  • Week4では以下を学ぶ
    • もっと高速にかつSuffixTreeに依存せずにSuffixArrayを構築する方法
    • SuffixArrayとLCPArrayから高速にSuffixTreeを構築する方法

Construct Suffix Array (Manber & Myers)

  • このアルゴリズムでは部分文字列のソート結果を用いながら接尾辞配列を求めていく
  • S = ababaa$ の suffix array をもとめる例(sa[i]はSuffixArray)
sa[i] S[sa[i]:]
6 $
5 a$
4 aa$
3 baa$
2 abaa$
1 babaa$
0 ababaa$
  • この sa[i] を S[sa[i]] の辞書順序に並べるのが目標
  • Manber & Myers のアルゴリズムでは、各位置からk文字の部分文字列のrankから2k文字の部分文字列のrankを求めるのを繰り返し、その部分文字列の長さが元の文字列の長さを超えたら終了
    • rankは、ある長さの部分文字列が、同じ長さの部分文字列の中で辞書順に並べて何番目に小さいか
    • k=1からスタート

各位置から1文字の部分文字列をソート

  • 各位置から1文字の部分文字列たちの順番を計算して S[sa[i]:sa[i]+1] を辞書順にソート
    • [例] S[1:3] は Sの1文字目~3文字目の部分文字列を表す
  • rank[sa[i]] は S[sa[i]:sa[i]+1] が何番目に(辞書順で)小さいか
  • rank[sa[i]+1] のうち、sa[i]+1 > 6 の場合 -1 に
    • rank[sa[i]+1] は、S[sa[i]:sa[i]+1]の後ろ1文字のrank
i sa[i] S[sa[i]:sa[i]+1] rank[sa[i]] rank[sa[i]+1]
0 6 $ 0 -1
1 0 a 1 2
2 2 a 1 2
3 4 a 1 1
4 5 a 1 0
5 1 b 2 1
6 3 b 2 1

各位置から2文字の部分文字列をソート

  • 上の図の rank[sa[i]] と rank[sa[i]+1] に注目
  • rank[sa[i]] が異なる部分は順序がわかりきってるのでソートせずそのまま、rank[sa[i]]が同じ部分にのみ注目する
  • rank[sa[i]] が同じとき、それぞれの後ろの文字のrankは rank[sa[i]+1]を見ればわかる
    • rank[sa[i]] と rank[sa[j]] の比較は S[sa[i]:sa[i]+1] と S[sa[j]:sa[j]+1]の比較と同値
  • よって上の図のrank[sa[i]]とrank[sa[i]+1]の辞書順序でソートすることで直接S[sa[i]:sa[i]+2]どうしを比較しなくてもソートが実現出来る
    • 下のsa[i]、S[sa[i]:sa[i]+2]はソートした結果
  • rankを更新
    • old_rank[sa[i]] と old_rank[sa[i]+1] を辞書順序をソートしたときの何番目に小さいか
sa[i] S[sa[i]:sai[i]+2] old_rank[sa[i]] old_rank[sa[i]+1] new_rank[sa[i]] new_rank[sa[i]+2]
6 $ 0 -1 0 -1
5 a$ 1 0 1 -1
4 aa 1 1 2 0
0 ab 1 2 3 3
2 ab 1 2 3 2
1 ba 2 1 4 4
3 ba 2 1 4 1

各位置から4文字の部分文字列をソート

  • 同様に上の図の new_rank[sa[i]] と new_rank[sa[i]+2] に注目
    • あとは同様に
  • 各位置から8文字の部分文字列を...
  • Sの長さ(6)を超えたので終了
    • この時点での sa[i] が求めるべき Suffix Array となる
  • 文字列を実際に比較するのは各位置の1文字のみで、それ以降はそれぞれのrankという数字の比較によってsuffix arrayを求めることができる
  • 時間計算量O(|Text| * log(|Text|)) らしい(正直ピンとこない)

Construct LCP Array

文字列Sの、LCP(Longest Common Prefix) Array は 先ほど求めたSuffixArray sa[i]と LCP(srt1, str2)(str1とstr2のLCPを求める関数) から以下のように定義します

lcp[i] = LCP(S[sa[i]:], S[sa[i+1]:])
sa[i] S[sa[i]:] lcp[i]
6 $ 0
5 a$ 1
4 aa$ 1
2 abaa$ 3
0 ababaa$ 0
3 baa$ 2
1 babaa$ -

S[sa[i]:]とS[sa[i+1]:]とをひとつひとつ比べていくとLCPArrayの構築に時間計算量O(|Text|^2)かかる

kasai’s Algorithm

S=ababaa$

i sa[i] S[sa[i]:] rank[sa[i]] rank[i]
0 6 $ 0 4
1 5 a$ 1 6
2 4 aa$ 2 3
3 2 abaa$ 3 5
4 0 ababaa$ 4 2
5 3 baa$ 5 1
6 1 babaa$ 6 0
  • sa[rank[i]]: S[i:]の文字列中での開始位置
  • rank[i]: S[i:]のSuffixArray内での順番
  • S[sa[rank[i]-1]:]] はSffixArray内での一つ前の文字列
    • 例えば i=0 のとき S[i:] = ababaa$ で、rank[0]-1=3なのでS[sa[3]:]=abaa$ 確かに
  • Lemma
h[i] = LCP(S[i:], S[sa[rank[i]-1]:]) とすると
h[i+1] >= h[i] - 1
  • これは S[i:]とS[sa[rank[i]-1]:]のそれぞれの先頭1文字を削ったもの同士のLCP(h[i+1])はh[i]に対してたかだか1ずつしか減らない、もしくは増えることを意味する
  • [例1] h[0] = LCP(ababaa$, abaa$) = 3, h[1] = LCP(babaa$, baa$) = 2
  • [例2] h[3] = LCP(baa$, ababaa$) = 0, h[4] = LCP(aa$, a$) = 1
  • h[i] > 0 のときは h[i+1] = h[i] - 1、h[i] = 0 のときは h[i+1] > h[i] になる感じかな？
  • 文字列中の位置0の接尾辞から初めて、位置を1,2,..と順番に、LCP(S[i:], S[sa[rank[i]-1]:])を計算していくのだが、上記の性質により実際に文字同士を比較する回数を減らすことができる。
  • i>1に対して、|h[i-1]-1|までは共通部分文字列なのはわかってるので、比較するのは|h[i-1]-1|+1番目の文字以降のみで良い
    • (h[i-1]の-1は先頭1文字を削ることによるLCPの減少)
  • lcp[rank[i]-1] = h[i] となる
    • rank[i]-1 はS[sa[rank[i]-1]:] の接尾辞配列での順番
i S[i:] S[sa[rank[i]-1]:] h[i] 備考 rank[i]-1
0 ababaa$ abaa$ 3 LCPを計算するとh[0]=3 3
1 babaa$ baa$ 2 3文字目から比較 b vs a なので終了 5
2 abaa$ aa$ 1 2文字目から比較 b vs a 2
3 baa$ ababaa$ 0 1文字目から比較 b vs a 4
4 aa$ a$ 1 1文字目から比較 aa vs a$ なので h[i]=1 1
5 a$ $ 0 1文字目から比較 a vs $ 0

時間計算量 O(|S|) で計算できる

Suffix Array + LCP Array -> Suffix Tree

各ノードはdepth (root node からそのノードを辿るまでの文字数)などの属性を持つ

  • まずは root node を作成 (depth = 0)
  • lcpPrev = 0, curNode = root とする
  • i=0..|Text|
    • lcpPrev >= curNode.depth になるまで curNode を親へと登らせていく
    • 停止した時点での curNode.depth と lcpPrev の値によって処理が変わる
    • lcpPrev = curNode.depth の場合
      • curNode の下に新しく葉ノードを作り、それをcurNodeに
    • lcpPrev > curNode.depth の場合
      • curNodeと、辿ってきた子ノードと、の間に中間ノードを作る
        • curNodeと子ノード間エッジの文字列をSとする
        • curNodeと中間ノード間エッジの文字列はS[:lcpPrev]
        • 中間ノードと子ノード間エッジの文字列は S[lcpPrev:]
      • 中間ノードの下に新しく葉ノードを作り、それをcurNodeに
    • lcpPrev = lcp[i] (if i < |Text|)

ababaa$のSuffixArrayとLCPArrayからSuffixTreeを構築する例を考えてみる

i sa[i] S[sa[i]:] lcp[i]
0 6 $ 0
1 5 a$ 1
2 4 aa$ 1
3 2 abaa$ 3
4 0 ababaa$ 0
5 3 baa$ 2
6 1 babaa$ -

i=1の例
$ のみから Trie が構築されている状態 a$ を挿入しようとしている

f:id:tanishiking24:20170105095400p:plain

  • lcpPrev=0(=lcp[i-1]), curNodeはxノード
  • curNode.depth > lcpPrev なので親(root)をcurNodeとする
    • lcpPrev >= curNode.depth(=0) なのでここで停止
  • lcpPrev = curNode.depth なので curNode(root) の下に新しく葉ノードyを作る

f:id:tanishiking24:20170105095415p:plain

i=2の例

  • aa$ を挿入する
  • lcpPrev=1 curNodeは i=1 のときに作成した yノード
  • curNode.depth > lcpPrev なので親ノードrootをcurNodeとする
    • lcpPrev >= curNode.depth(=0) なので停止
  • lcpPrev(=1) > curNode.depth(=0) なので
    • curNodeと子ノードyの間に中間ノードmidを作成(元のエッジの文字列はa$)
      • curNodeと中間ノードmid間のエッジ文字列は "a$"[:lcpPrev]="a"
      • 中間ノードmidと子ノードy間のエッジ文字列は "a$"[lcpPrev:]="$"
    • 新しく葉ノードzを作って中間ノードmidの子に

f:id:tanishiking24:20170105095454p:plain

おわりに

文字列処理アルゴリズムをいろいろと学んだが、どちらかというと古典的/基本的な手法を教えてくれる授業だったのかな
各種データ構造のもっと時間/空間で効率の良い構築アルゴリズムはこの授業ではやらなかったので、次はそれらを学んで実装したいなと思ってます
この記事を読んで各アルゴリズムの雰囲気を掴んでもらえたら幸いです、実際に実装してみよう！という場合は多分この記事だけでは役不足だと思うので是非Courseraのこのコースを受講してみてください

www.coursera.org