Deep Learning を勉強しようと思い、Coursera の Deep Learning Specialization を受講し始めた。
- ある手法がうまくいく/うまくいかないことのイメージを説明してくれたり、実装に際してのtips and tricksも教えてくれるのが良い。
- 解析や線形代数を知らない人にも門戸を開くために、コスト関数やactivation functionの微分の計算などは答えだけ提示している。(良いと思う)
- 穴埋め形式ではあるのものの、Jupyter Notebook 上で自分で Neural Network を実装する課題があって面白い。
この専門講座は5つのコースから構成されていて、Neural Networks and Deep Learning はその1つ目のコース。内容としてはロジスティック回帰、単層ニューラルネット、2層ニューラルネット、L層ニューラルネット。
授業で聞いたポイントや、授業で触れられていない数学的な部分をメモしておく。授業内容そのものについてはあまり触れない。あくまで個人用のメモ
Python Basics with numpy
shape
np.random.randn(5, 1) # shape = (5, 1) 5 x 1 行列 # [[ 1 ], # [ 2 ], # [ 3 ], # [ 4 ], # [ 5 ]]
reshape
v.shape # (x, y, z, examples) v_flattened = v.reshape(x * y * z, examples) v_flattened # (x * y * z, examples)
# 0-th data を除いて flattening する # ドキュメントにも書いてないように見えるけど...? # The "-1" makes reshape flatten the remaining dimensions ndarray.reshape(ndarray.shape[0], -1)
機械学習のコードを書いているとndarray(や pandas DataFrame)のshapeが合わずに実行時エラーが起きることが多いので、適宜shapeに対してassertionを挟んでやるとデバッグしやすい。
assert(a.shape == (5, 1)) assert(a.shape[1] == b.shape[1])
rank-1 array
a = np.random.randn(5) # a.shape = (5,) <- rank 1 array # rank 1 array は column vector としても row vector としても振る舞うので扱いが難しい # shapeが明示的に決まったndarrayを使うのが吉 a.reshape(5,1) # などで明示的な行列に変換可能
axis
Axes are defined for arrays with more than one dimension. A 2-dimensional array has two corresponding axes: the first running vertically downwards across rows (axis 0), and the second running horizontally across columns (axis 1).
x = np.arange(12).reshape((3,4)) # array([[ 0, 1, 2, 3], # [ 4, 5, 6, 7], # [ 8, 9, 10, 11]]) x.sum(axis=0, keepdims=True) # running vertically #[[12 15 18 21]] x.sum(axis=1, keepdims=True) # running horizontally #[[ 6] # [22] # [38]]
dtypes
NumPyのデータ型dtype一覧とastypeによる変換(キャスト) | note.nkmk.me
broadcasting
ndarray と、スカラー値もしくはある方向の要素数が1のndarray(他の方向のshapeは一致してる必要がある)との間で演算を行う場合、自動的に値がコピーされ、shapeが一致するように計算される。
When operating on two arrays, NumPy compares their shapes element-wise. It starts with the trailing dimensions and works its way forward. Two dimensions are compatible when 1. they are equal, or 2. one of them is 1
a = np.array([[1, 2, 3], [4, 5, 6]]) a + 1 #[[2, 3, 4] # [5, 6, 7]] b = np.array([[100], [100]]) a + b #[[101, 102, 103] # [104, 105, 106]]
vectorization
行列計算には numpy.dot 等を使い、explicit for-loop を使わない。
import numpy as np a = np.random.rand(100000) b = np.random.rand(100000) c = np.dot(a, b) # 早いし、ベクトルのサイズ増やしても速度は変わらない(O(1)) # for loop だと O(N) の計算量になる。 # numpy vectorization では内部で SIMD命令が(利用可能なら)使われるので高速
Logistic Regression
授業では数学的な部分はあまり無かったので、はじパタを参照しつつ導出

- 作者:平井 有三
- 発売日: 2012/07/31
- メディア: 単行本(ソフトカバー)


softmax の微分は手を動かすとわかりやすい
further reading: The Softmax function and its derivative - Eli Bendersky's website
最適解を解析的に導出できないので、gradient discent や 共役勾配法で最適解を探索
Shallow Neural Network (~2層)
Activation function 色々
- activation function には非線形関数を利用する。
この動画わかりやすい & 面白い
結合係数はランダム値で初期化する(0で初期化しない)
- すべて0で初期化すると、後続のレイヤーの素子への入力及び出力はすべて同じになってしまう。
- その結果学習をすすめたところで各レイヤ内の素子からの出力はすべて同じになり、素子の数を増やしてもニューラルネットの表現力は向上しない。
Loss function の結合係数による微分
Loss function には MSE を使ってるけれど、授業では交差エントロピー誤差使ってる。どのLoss functionを選べばよいかは後で
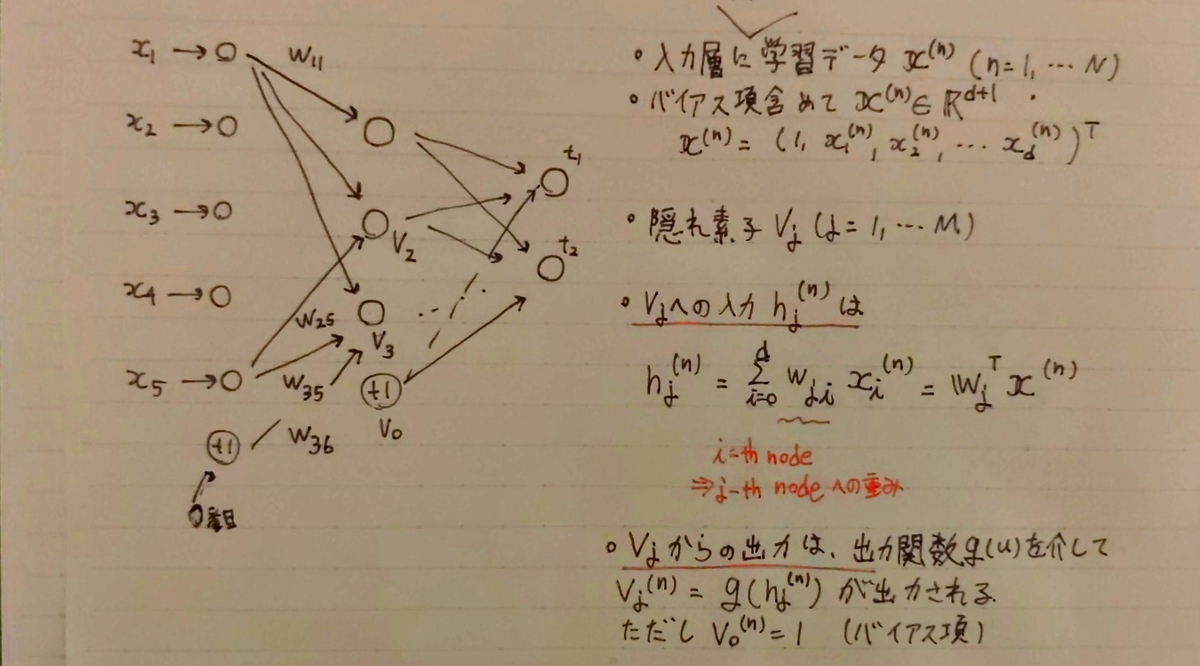


多層ニューラルネットでは隠れ層-出力層の結合係数だけでなく、入力層-隠れ層の結合係数も当然学習する必要があるのでそっちでも微分

Deep Neural Network
層を重ねることでニューラルネットの表現力が上がる直感
- 入力層に近い層で細かい部分の特徴を捉え、それを合成していくことで表現力高く特徴を捉えることができる
- 例えば画像認識の場合は、入力層に近いところではエッジなどが検出され、それを合成していくことで最終的に捉えたい複雑なパターンを認識できるようになるイメージ
- とはいえ隠れ層を増やせばいいわけではない
- 計算コストが大きくなる(当然)
- オーバーフィッティング
- ホールドアウトearly-stoppingや正則化項の導入でオーバーフィッティングを防ぐ(詳細は次のコースで)
Deep Neural Network での forward / backward propagation
基本的に2層ニューラルネットと変わらない(計算する数が増えただけ)

書いている通り、後ろの層で計算した微分を、その前の層の微分にどんどん利用していく。こう書くと誤差逆伝搬というのがなるほどたしかにという感じがする。
行列による微分に慣れないので、バッチ処理しない場合でベクトルによる微分を考えてもわかりやすい。
メモ
Loss Function には何を選べば良い?
パラメータの初期化など
次の Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization | Coursera で詳しく説明されるが簡単に
- 結合係数の初期値は小さく設定する
- 授業では
np.random.randn(n2, n1) * 0.01 - 結合係数が大きいと、linear product の値が大きくなる。その結果 sigmoid や tanh の勾配は非常に小さいものとなり学習が進まない(勾配消失問題の原因の一つ)
- 同様の理由でデータの値も正規化してやると学習が早く進む。
- 授業では